The Runge-Kutta method is a class of important algorithms for numerically solving differential equations, and it has been widely used in many fields of science and engineering. The stability of the Runge-Kutta method has a decisive influence on its numerical results.
For a long time, understanding and characterizing the Runge-Kutta method’s stability has been an important fundamental issue in the field of numerical analysis. The research in this area has attracted the attention of many computational mathematicians. Many classical theories have been developed, such as the stability region theory based on the linear scalar Dahlquist equation, the algebraic stability theory for nonlinear systems, etc.
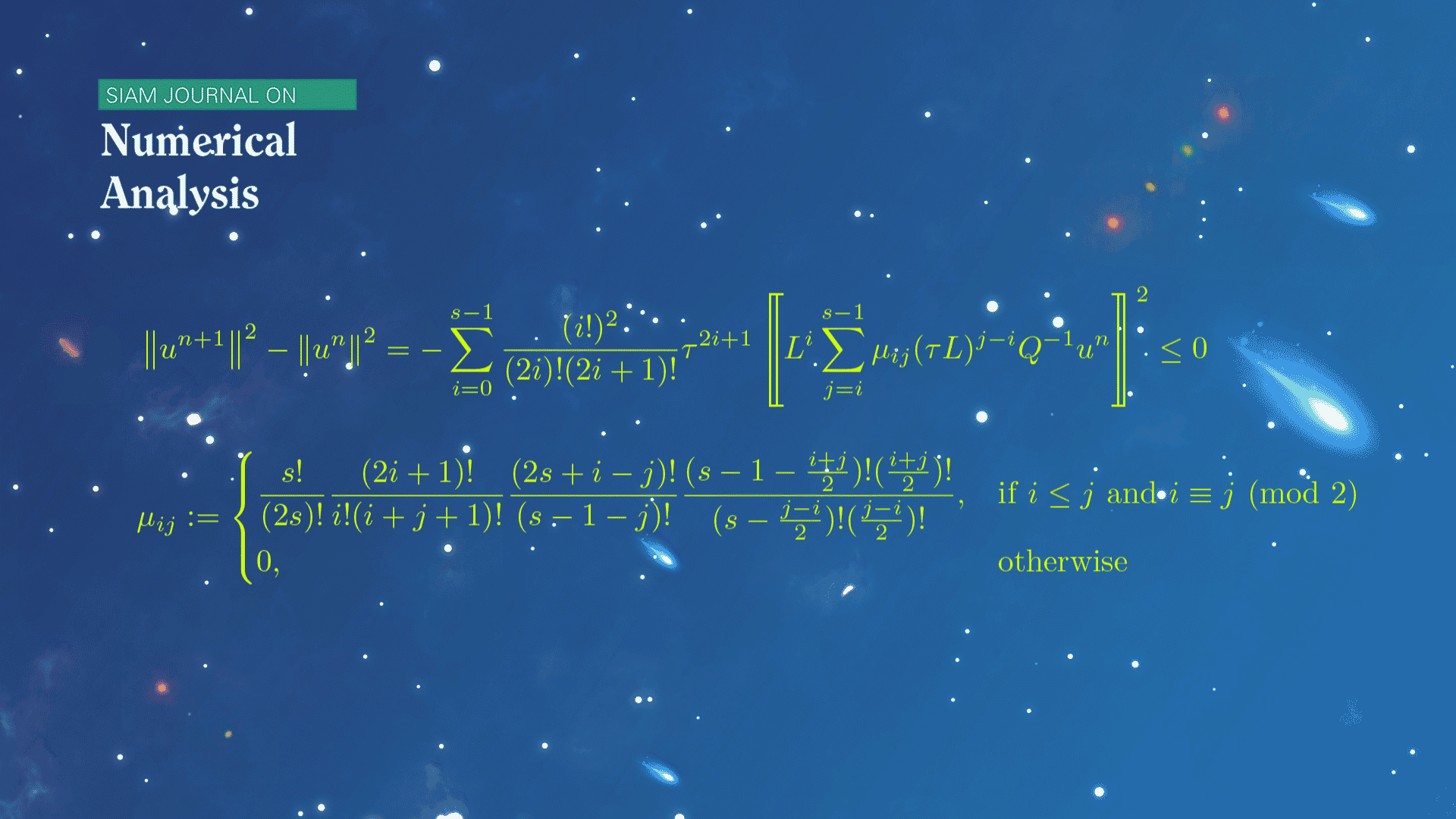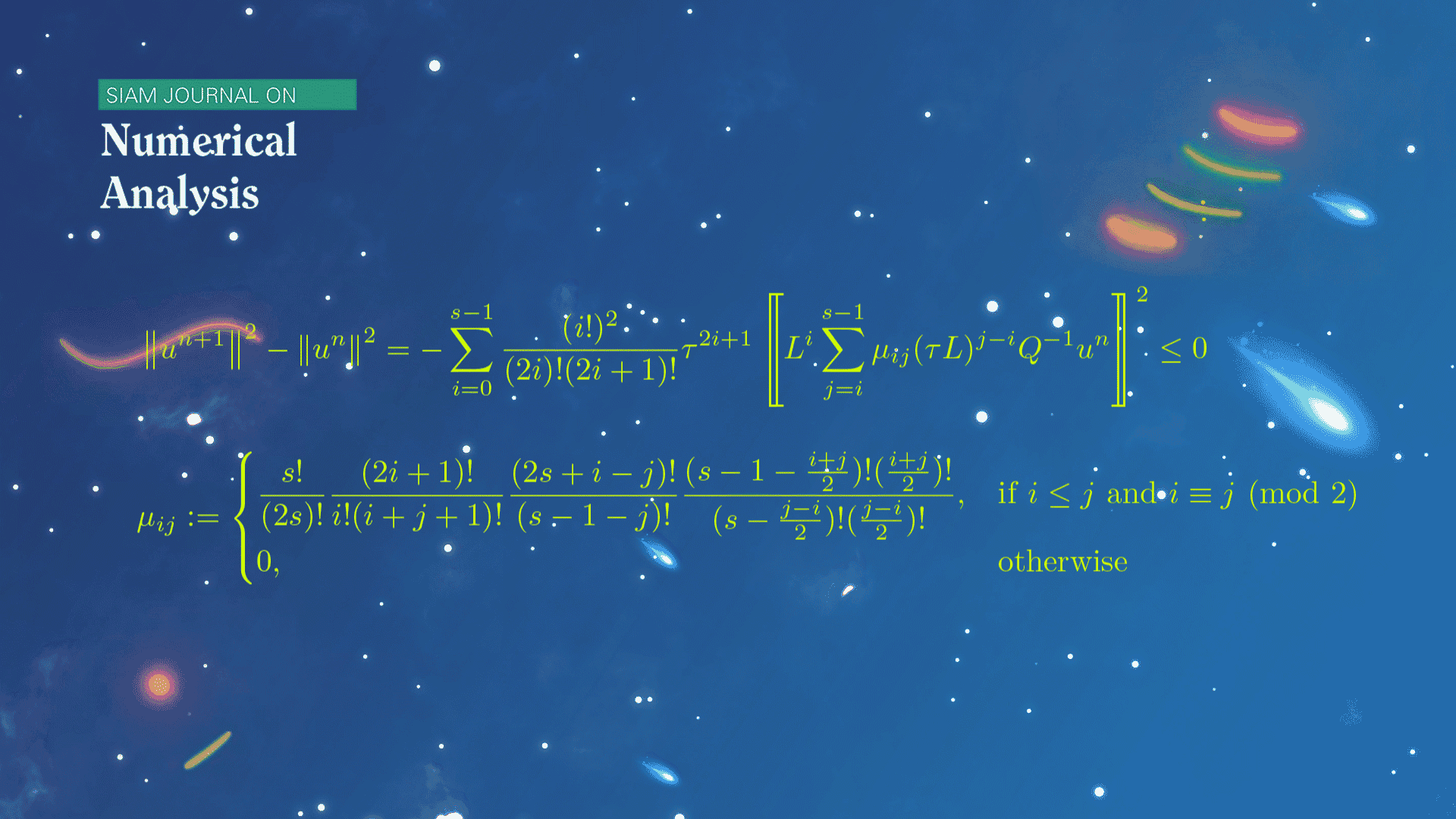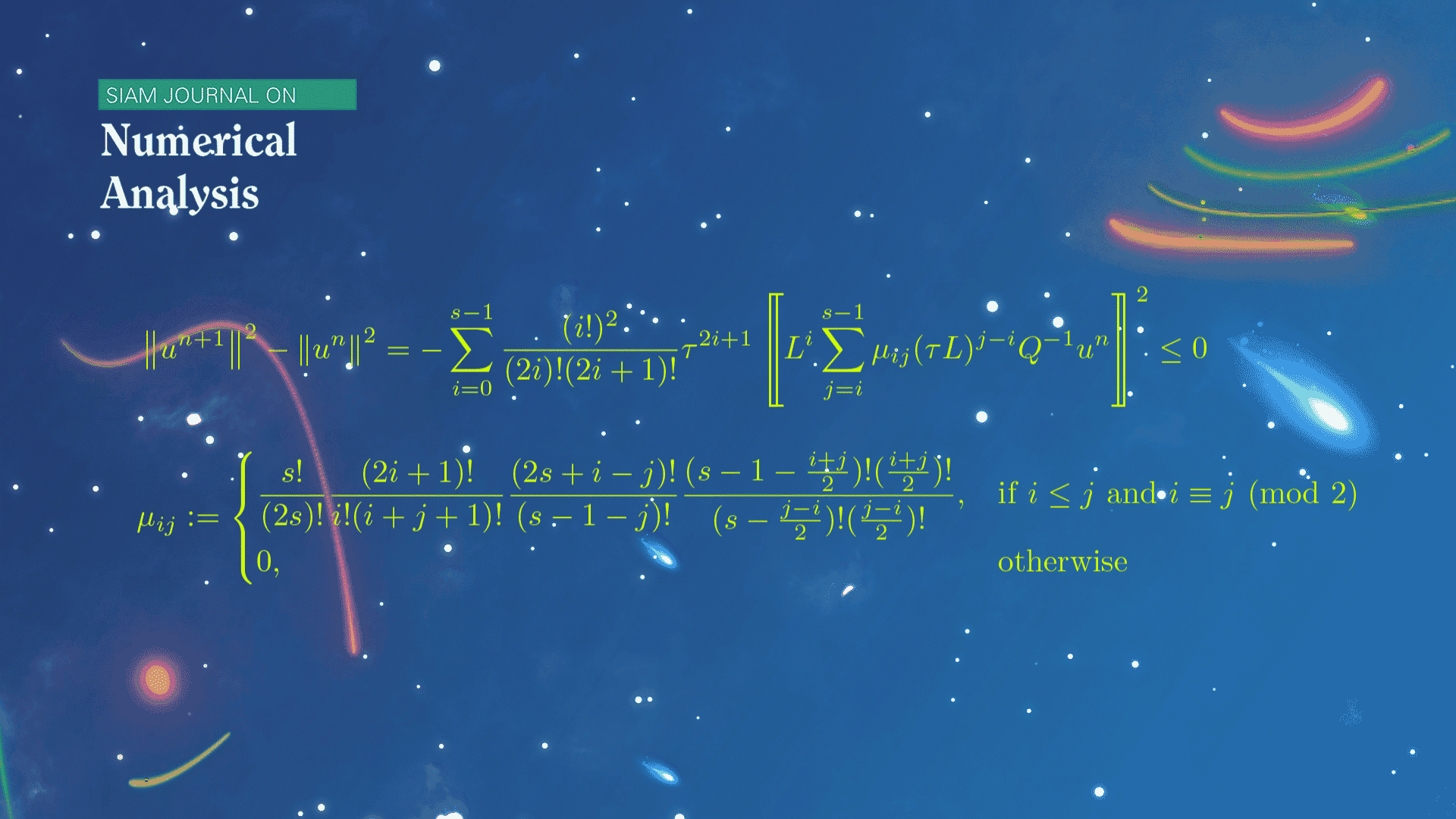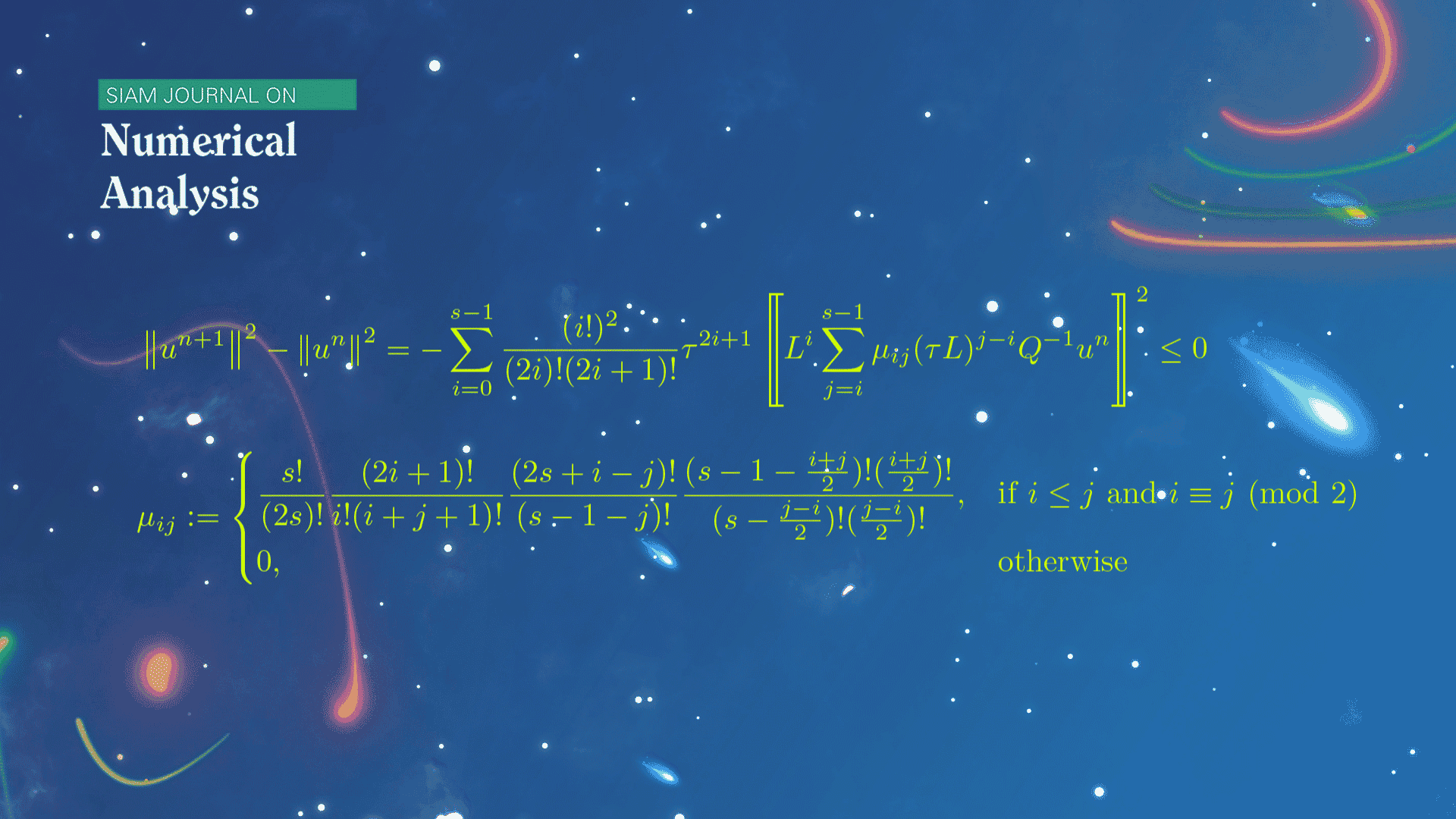
Yuanzhe Wei, an undergraduate student in the Department of Mathematics at the Southern University of Science and Technology (SUSTech), and his advisor, Kailiang Wu, Associate Professor of the Department of Mathematics at SUSTech, in collaboration with Professor Zheng Sun of the University of Alabama (UA), have achieved important results in the research on the stability of Runge-Kutta method.
Their research paper, entitled “On Energy Laws and Stability of Runge-Kutta Methods for Linear Seminegative Problems,” was published in the SIAM Journal on Numerical Analysis, a top journal in computational mathematics.
Their research focuses on a general linear semi-negative definite system, and studies the energy evolution law of the numerical solution given by the Runge-Kutta method from a new perspective. Inspired by the integration by parts technique and the law of energy dissipation in the continuous system, this article establishes a theoretical framework for deriving the discrete energy identities for general explicit and implicit Runge-Kutta algorithms, providing criteria for their strong/weak stability.
This work also carefully studies a class of Runge-Kutta algorithms corresponding to the diagonal Padé approximation. Based on the hypergeometric series technique and several technical combinatorial identities, the unified energy identity of such algorithms of arbitrary order is established. This discrete energy identity has a similar structure to the energy identity of the continuous problems, revealing the intrinsic relation between the continuous and discrete energy laws.
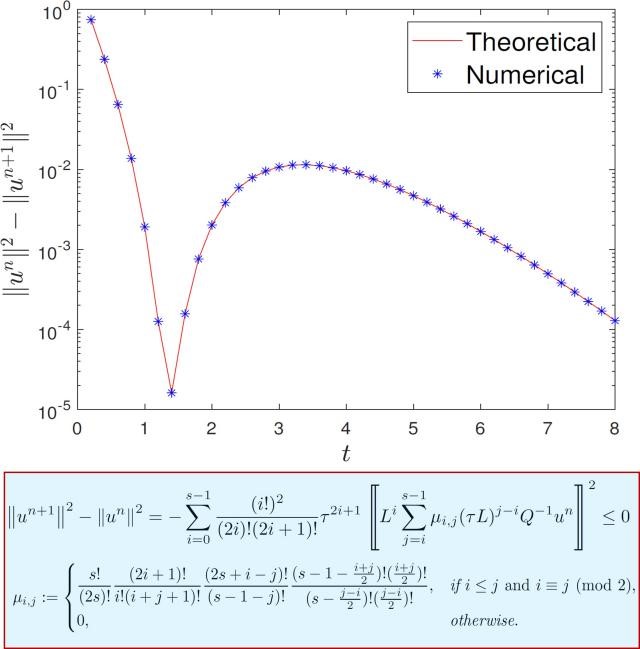
Figure 1. The discovered discrete energy identity for diagonal Padé approximations
The contribution by Yuanzhe Wei mainly lies in the challenging discovery of Theorem 5.1 in the paper, where he analytically constructs and proves the Cholesky-type decomposition of a class of complicated positive definite matrices, thereby deriving discrete energy identities for diagonal Padé approximation of arbitrary order.
Yuanzhe Wei, Assoc. Prof. Kailiang Wu, and Prof. Zheng Sun are the co-first-authors of this paper. Prof. Kailiang Wu is the corresponding author, and SUSTech is the corresponding affiliation.
This work was partially supported by the National Natural Science Foundation of China (NSFC).
Paper link: https://epubs.siam.org/doi/10.1137/22M1472218