1st East Asia Symposium of IPIA Programme
Jan 24-Mar 1, 2016
Conference Summary
outh University of Science and Technology, Shenzhen, China
Feb. 29-Mar. 1, 2016
Venue: Room 706, Service Center for Teaching and Research(教学科研中心)
Organizing Committee:
Jingzhi Li, South University of Science and Technology Hongyu Liu, Hong Kong Baptist University
Gunther Uhlmann, University of Washington, Seattle & Hong Kong University of Science and Technology
Jenn-Nan Wang, National Taiwan University
Bo Zhang, Institute of Applied Math, Chinese Academy of Sciences Jun Zou, Chinese University of Hong Kong
Contact: Airong Liu (刘爱容)18929302017 liuar@sustc.edu.cn Zhenyu Wen (温珍玉)1882429201 wenzy@mail.sustc.edu.cn
Abstracts
1.Eemeli Blasten, Hong Kong University of Science and Technology Title: Non-scattering energies, new resolvent estimates and other projects
Abstract: I will introduce myself and talk about most of my past and present work in a non-technical way. My previous work was on three topics: the 2D inverse problem for the Schrödinger equation, transmission eigenvalues and non- scattering energies. Presently I'm working on several projects:
l proving Green's function estimates for general constant coefficient PDEs
l non-scattering energies in the hyperbolic space
l understanding the solution to inverse backscattering by Rakesh and Uhlmann
l 1D networked inverse problem for water pipe systems (with real engineers!)
l making LaTeX-quality documents for the web
The talk will mostly focus on the mathematics related to scattering theory and less on the last two topics.
2.Catalin Carstea, National Taiwan University
Title: Uniqueness for the two dimensional Calderon problem with singular conductivity
Abstract: In this talk I will discuss the uniqueness question for Calderon's problem in two dimensions for conductivities in W^{1,2} whose Sobolev norm is small. Even with the smallness condition this allows for unbounded conductivities.
3.Xiaofei Li, Inha University, Korea
Title: Matched asymptotic analysis to solve the narrow escape problem in a domain with a long neck
Abstract: In this study, we mainly consider the narrow escape problem in a two-dimensional domain $\Omega$ with a long neck, which is the
two-dimensional analogue of a dendritic spine geometry. The narrow escape problem requires the computation of the mean escape time of a Brownian particle starting from the head until it exits from the end of the neck, where the particle is absorbed. We divide the domain into the neck part $\Omega_n$ and the head part $\Omega_h$, with the common boundary $\Gamma_{\varepsilon}$. The escape time in $\Omega_h$ can be considered to be the time from the head to the end of the neck, while the escape time in $\Omega_n$ can be considered to be the time from the neck to the end of the neck. We compute the two exit times separately and match them by considering some boundary value problem with an impedance boundary condition on $\Gamma_{\varepsilon}$, which we refer to as the Neumann-Robin boundary model.
4.Yi-Hsuan Lin, National Taiwan University
Title: The enclosure method for the anisotropic Maxwell system Abstract: We develop an enclosure-type reconstruction scheme to identify penetrable and impenetrable obstacles in electromagnetic field with anisotropic medium in \mathbb{R}^{3}. The main difficulty in treating this problem lies in the fact that there are so far no complex geometrical optics solutions available for the Maxwell's equation with anisotropic
medium in \mathbb{R}^{3}. Instead, we derive and use another type of special solutions called oscillating-decaying solutions. To justify this scheme, we use Meyers' L^{p} estimate, for the Maxwell system, to compare the integrals coming from oscillating-decaying solutions and those from the reflected solutions.
5.Jian Lu, Shenzhen University, Shenzhen
Title: An exp-model and its fixed-point proximity algorithm for multiplicative noise removal
Abstract: We propose a variational model for restoration of images corrupted by multiplicative noise. The proposed model formulated in the logarithm transform domain of the desirable images consists of a data fitting term, a quadratic term, and a total variation regularizer. The data fitting term results directly from the presence of the multiplicative noise and the quadratic term reflects the statistics of the noise. We show that the proposed model is strictly convex under a mild condition. The solution of the model is then characterized in terms of the fixed-point of a nonlinear map described by the proximity operator of a function involved in the model. Based on the characterization, we present a fixed-point proximity algorithm for solving the model and analyze its convergence. Our numerical results indicate that the proposed model compares favorably to several existing state-of-the-art models with better results in terms of the peak signal-to-noise ratio of the denoised images and the CPU time consumed.
6.Yuliang Wang, Hong Kong Baptist University
Title: A Gesture-based Instruction and Input Device Using Acoustic Waves
Abstract: A novel method is proposed for the recognition of gestures
using acoustic waves. The gestures are modeled by acoustic scatterers whose shapes are drawn from a prescribed dictionary and the recoginition is modeled as an inverse acoustic scattering problem. The incident wave is generated from a fixed point exterior of the scatterer and the scattered field is measured at a bounded surface containing the source point. The recognition algorithm consists of two steps and requires two incident wave of different wavenumber. The approximate location of the scatterer is firstly determined by using the measured data at small wavenumber and the shape of the scatterer is then identified using the computed location of the scatterer and the measured data at a regular wavenumber. Numerical experiments show the proposed method is computationally efficient and works with full or phaseless backscattering data of small aperture.
7.Jiaqing Yang, Xi’an Jiaotong University, Xi’an
Title: Determination of coefficients in Helmholtz equations for periodic structures
Abstract: In this talk, I will discuss an inverse problem of determining the coefficient for the Helmholtz equation from the near-field data in the periodic case. I will show under some certain conditions that the index of refraction or at least its support in a multi-layered media is completely recovered, using partial scattering field data measured only from one side of the total structure, corresponding to a countably infinite number of downward propagating incident plane waves.
8.Qi YE, South China Normal University, Guangzhou
Title: Kernel-based Methods for Deterministic or Stochastic Data Abstract: This talk gives a new insight of kernel-based methods to solve the deterministic or stochastic problems such as (stochastic) partial
differential equations. We will combine the techniques of meshfree approximation and kriging interpolation to restudy the kernel-based methods for the scattered data approximation. Generally, we will combine the knowledge of approximation theory, statistical learning, probability theory, and stochastic analysis into one theoretical structure. The main idea is to endow the Sobolev spaces with the probability measures induced by the positive definite kernels such that the Gaussian random variables can be well-defined on the Sobolev spaces. The constructions of these Gaussian random variables will provide the kernel-based estimators for the deterministic or stochastic data.
This work is joint with Leevan Ling at HKBU.
9.Haizhang Zhang, Sun Yat-sen University, Guangzhou
Title: Hyper-Gaussian Regularized Whittaker-Kotel'nikov-Shannon Sampling Series
Abstract: The reconstruction of a bandlimit function from its finite sample data is fundamental in signal analysis. It is well-known that oversampling of a bandlimited function leads to linear convergence in its reconstruction. A simple and efficient Gaussian regularized Shannon sampling formula has been proposed with such a linear convergence ability. We show that all hyper-Gaussian regularized formula share this desired property. The analysis is built on estimates on the Fourier transform of the hyper-Gaussian functions.
This work is joint with Yang Wang at HKUST.
Traffic Information
By Metro: Tanglang Station(塘朗站), Huanzhong Line; School gate 1 (一号门) is 500m from Exit C of Tanglang Metro Station
By Bus: SUSTC Station(南方科技大学站) , Line M369, 43, 74, 81
Taxi: Southern University of Science and Technology in Tanglang(塘朗), Nanshan District
Address: No 1088, Xueyuan Rd., Xili, Nanshan District, Shenzhen, Guangdong, China 518055
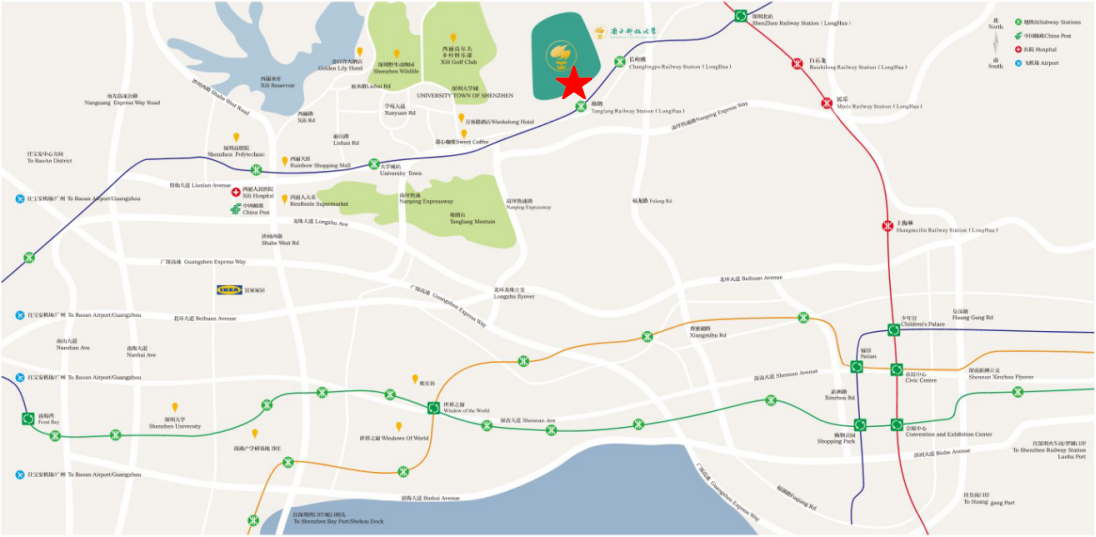
Campus Map
Hotel Information and Check-in
l Guest House 1(专家公寓1)
l Front Desk Telephone„86-0755-88015773
l Show your ID card or passport for hotel check-in